AVL TREE
Definisi
AVL Tree adalah subtipe dari BST atau yang biasa disebut sebagai Binary Search Tree. AVL sendiri diciptakan oleh tiga orang, yaitu Adelson, Velskii, dan Landis. AVL sendiri diciptakan untuk melakukan "self-balancing" antara anak kanan dengan anak kiri, agar waktu yang dibutuhkan dalam melakukan proses searching lebih singkat, sehingga program dapat berjalan lebih cepat. Untuk menetapkan tingginya dapat menggunakan rumus O(log n)
Syarat AVL
AVL Tree sendiri memiliki satu syarat penting yaitu perbedaan level atau kedalaman antara ruas kiri dengan kanan tidak boleh melebihi dari satu. Bila melebihi dari satu, maka akan melakukan "rebalancing" secara otomatis. Untuk menghitung perbedaan antara ruas kiri dengan ruas kanan, dapat dilakukan dengan menghitung balance factor (BF).
Balance Factor sendiri memiliki rumus sebagai berikut:
BalanceFactor(N) = Level (Subtree bagian kiri (N)) - Level (Subtree bagian kanan (N))
BalanceFactor(N) merupakan elemen dari {-1, 0, 1}
Berikut adalah contoh dari Balance Factor
Insert
Insert sendiri memiliki prinsip yang sama dengan Binary Search Tree, dimana node yang baru masuk, dijadikan sebagai leaf. Namun terdapat perbedaan dengan BST, bila dimasukkin node baru, maka akan melakukan penyeimbangan antara ruas kanan dengan ruas kiri.
Contohnya sebagai berikut:
1.
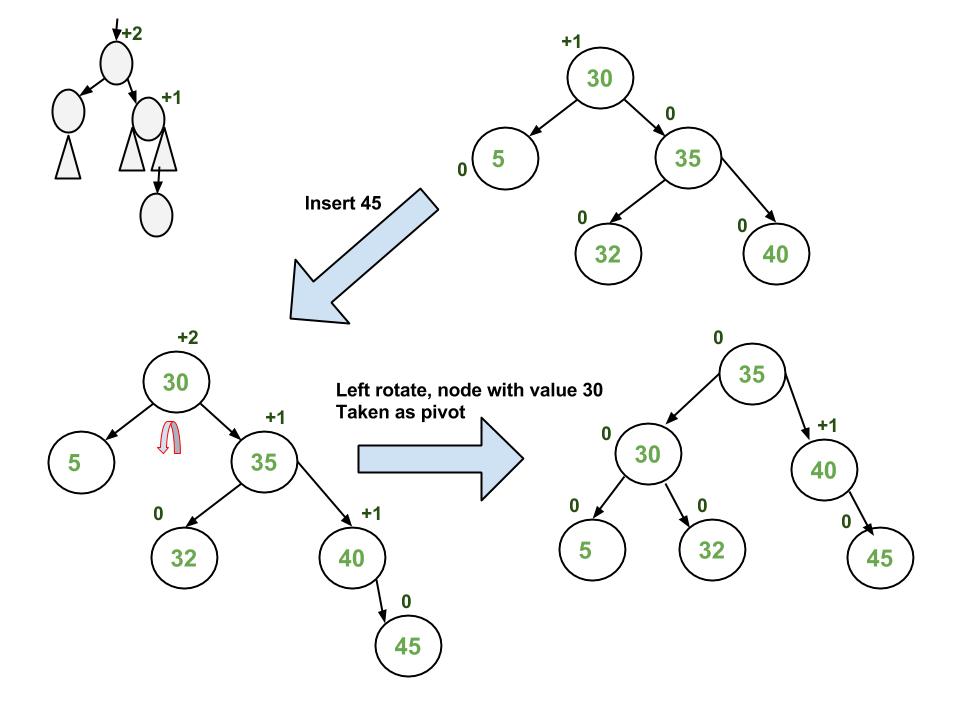
Pada gambar diatas, terdapat sebuah tree yang ditambahkan node yang berisi nilai 45. Node 45 menjadi anak kanan dari 40, karena 45 lebih besar dari 40. Namun bila terjadi hal tersebut, maka balance factor di root akan menjadi +2 atau -2, dikarenakan ruas kanan dari root memiliki kedalaman 3, sedangkan ruas kiri dari root memiliki kedalaman 1. Karena tidak seimbang, maka dilakukan self-balancing dengan cara mencari bagian yang rusak. Seperti yang diketahui, di root mengalami balance factor yang berbeda, dan angka 45 sangatlah mengganggu. Oleh karena itu, 3 node teratas dilakukan rotation ke left atau yang biasa disebut dengan left rotate. 30, 35, dan 40 di rotater ke arah kiri, sehingga 35 menjadi root, anak kirinya adalah 30, dan anak kanannya adalah 45. Ini sudah balance, dan dapat disebut sebagai single rotation.
2.
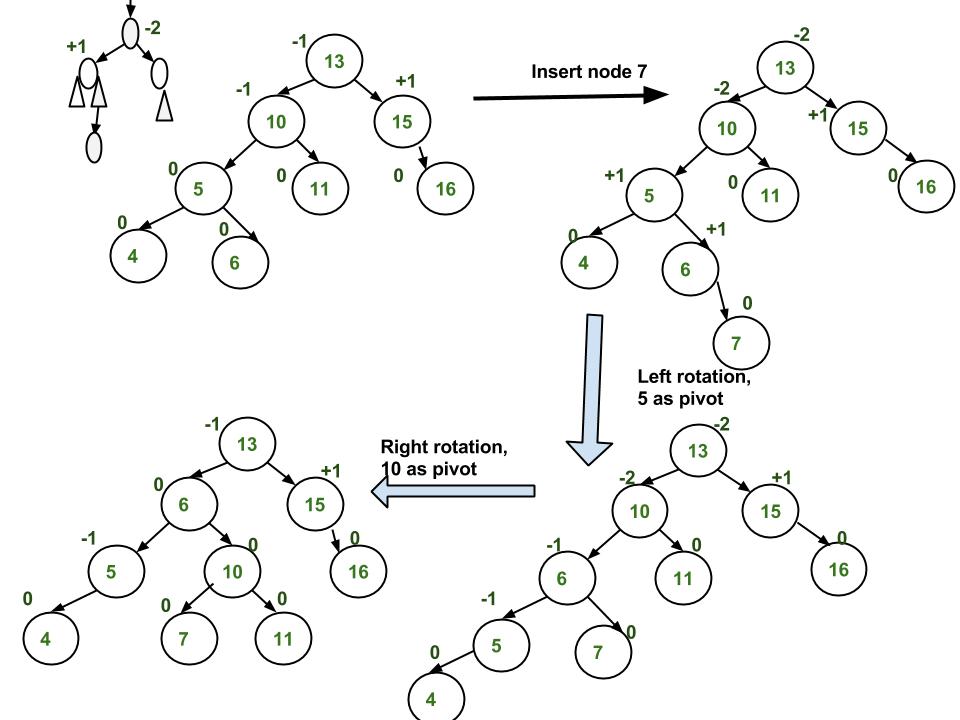
Pada gambar diatas, terdapat sebuah tree yang ditambahkan node yang berisi nilai 7. Node 7 menjadi anak kanan dari 6, karena 7 lebih besar dari 6. Namun bila terjadi hal tersebut, maka balance factor di root akan menjadi +2 atau -2 dan di anak kiri root balance factor akan menjadi +2 atau -2, dikarenakan ruas kiri dari root memiliki kedalaman 4, sedangkan ruas kanan dari root memiliki kedalaman 2 dan juga ruas kanan dari anak kiri root memiliki kedalaman 1, sedangkan ruas kiri dari anak kiri root memiliki kedalaman 4. Karena tidak seimbang, maka dilakukan self-balancing dengan cara mencari bagian yang rusak. Bagian yang pertama yang rusak adalah anak kiridari root, dan yang mengganggu adalah leaf yang memiliki nilai 7. Oleh karena itu angka 5, 6 ,7, kira rotate ke arah kiri atau yang biasa disebut sebagai left rotation untuk memperbaiki rantai. Setelah itu untuk memperbaiki 10 yang memiliki balance factor 2 atau -2, maka dilakukan rotasi kearah kanan atau yang biasa disebut sebagai right rotation. Ambil 3 node diatas dari 10, yaitu 10, 6 , dan 5 setelah itu melakukan right rotation. Setelah itu, 6 menjadi anak kiri dari root, dan tree sudah balance. Inidapat disebut sebagai double rotation.
Delete
Delete memiliki prinsip yang sama dengan Binary Search Tree. Bila ingin menghapus leaf, maka langsung hapus saja. Bila yang ingin dihapus memiliki child, maka child tersebut yang akan menggantikan node yang dihapus. Setelah melakukan delete, maka langkah berikutnya adalah melakukan self-balancing. Prosesnya sama seperti Insert, yaitu melakukan right rotation ataupun left rotation, dan juga bisa melakukan single rotation, maupun double rotation.

No comments:
Post a Comment