Ringkasan Final Data Structure
Data Structure
Nama : Isaac Andrean Yoshua
NIM : 2301927046
Kelas : CB01-CL
Lecturer : Ferdinand Ariandy Luwinda (D4522) dan Henry Chong (D4460)
Binary Search Tree
Pengertian
Sebelum masuk kedalam konsep Binary Search Tree, ada baiknya kita memahami konsep Tree itu sendiri. Tree adalah salah satu bentuk struktur data yang menggambarkan hubungan hierarki antar elemen-elemennya (relasi one to many).
Lalu apa perbedaannya dengan Binary Search Tree? Binary Search Tree adalah tree yang memiliki maksimal 2 percabangan saja, dan terdapat beberapa aturan. Child node sebelah kiri selalu lebih kecil daripada root node. Child node sebelah kanan selalu lebih besar daripada rootnode. Binary Search Tree biasa dikenal sebagai Sorted Version of Binary Tree.
Seperti pada gambar diatas, root node adalah 50, child node seblah kiri adalah 17, dan child node sebelah kanan adalah 76. Ini artinya child node sebelah kiri selalu lebih kecil dibandingkan root, dan child node kanan selalu lebih besar daripada root.
Operasi Binary Search Tree
Insert:
- Selalu dimulai dari root.
- Jika angka yang akan dimasukkan lebih kecil daripada sub tree, maka cek sebelah kiri dari sub tree. Bila kosong masukkan angka tersebut.
- Bila angka yang akan dimasukkan lebih besar daripada sub tree, maka cek sebelah kanan dari sub tree. Bila kosong, masukkan angka tersebut.
- Lakukan terus sampai menemukan node yang kosong untuk ditaruh sebuah nilai.
Deletion:
Untuk melakukan delete terdapat 3 situasi.
- Bila yang ingin dihapus di bagian leaf, dapat langsung dihapus. Pada gambar diatas, 12 dapat langsung dihapus.
- Bila yang akan dihapus memiliki satu child, hapus node tersebut dan gabungkan antara parent node tersebut dan child dari node tersebut. Pada gambar diatas, bila 72 dihapus, maka 54 menjadi parent 67.
- Bila yang akan dihapus memiliki dua child, cari sub tree bagian kiri kemudian dibandingkan dengan yang kanan. Pada gambar diatas, apabila angka 17 dihapus maka, angka 14 akan naik menggantikan posisi 17, angka 9 akan menjadi parent 12. Bila angka 50 yang dihapus, maka angka 23 akan naik menggantikan posisi 50, dann17 akan menjadi parent 19.
AVL Tree
Definisi
AVL Tree adalah subtipe dari BST atau yang biasa disebut sebagai Binary Search Tree. AVL sendiri diciptakan oleh tiga orang, yaitu Adelson, Velskii, dan Landis. AVL sendiri diciptakan untuk melakukan "self-balancing" antara anak kanan dengan anak kiri, agar waktu yang dibutuhkan dalam melakukan proses searching lebih singkat, sehingga program dapat berjalan lebih cepat. Untuk menetapkan tingginya dapat menggunakan rumus O(log n)
Syarat AVL
AVL Tree sendiri memiliki satu syarat penting yaitu perbedaan level atau kedalaman antara ruas kiri dengan kanan tidak boleh melebihi dari satu. Bila melebihi dari satu, maka akan melakukan "rebalancing" secara otomatis. Untuk menghitung perbedaan antara ruas kiri dengan ruas kanan, dapat dilakukan dengan menghitung balance factor (BF).
Balance Factor sendiri memiliki rumus sebagai berikut:
BalanceFactor(N) = Level (Subtree bagian kiri (N)) - Level (Subtree bagian kanan (N))
BalanceFactor(N) merupakan elemen dari {-1, 0, 1}
Berikut adalah contoh dari Balance Factor
Insert
Insert sendiri memiliki prinsip yang sama dengan Binary Search Tree, dimana node yang baru masuk, dijadikan sebagai leaf. Namun terdapat perbedaan dengan BST, bila dimasukkin node baru, maka akan melakukan penyeimbangan antara ruas kanan dengan ruas kiri.
Contohnya sebagai berikut:
1.
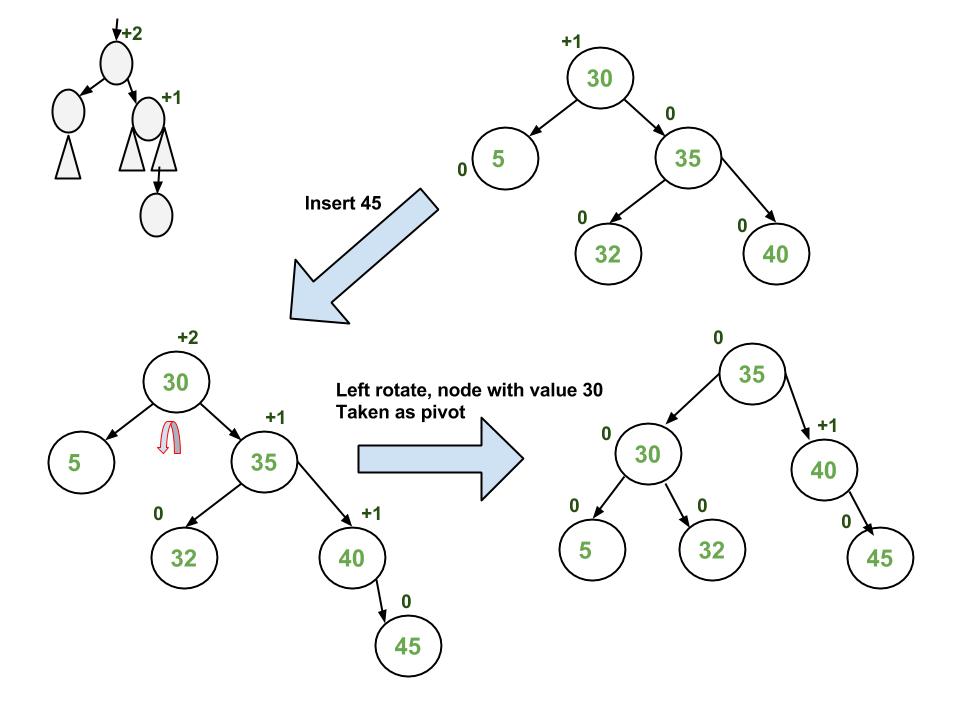
Pada gambar diatas, terdapat sebuah tree yang ditambahkan node yang berisi nilai 45. Node 45 menjadi anak kanan dari 40, karena 45 lebih besar dari 40. Namun bila terjadi hal tersebut, maka balance factor di root akan menjadi +2 atau -2, dikarenakan ruas kanan dari root memiliki kedalaman 3, sedangkan ruas kiri dari root memiliki kedalaman 1. Karena tidak seimbang, maka dilakukan self-balancing dengan cara mencari bagian yang rusak. Seperti yang diketahui, di root mengalami balance factor yang berbeda, dan angka 45 sangatlah mengganggu. Oleh karena itu, 3 node teratas dilakukan rotation ke left atau yang biasa disebut dengan left rotate. 30, 35, dan 40 di rotater ke arah kiri, sehingga 35 menjadi root, anak kirinya adalah 30, dan anak kanannya adalah 45. Ini sudah balance, dan dapat disebut sebagai single rotation.
2.
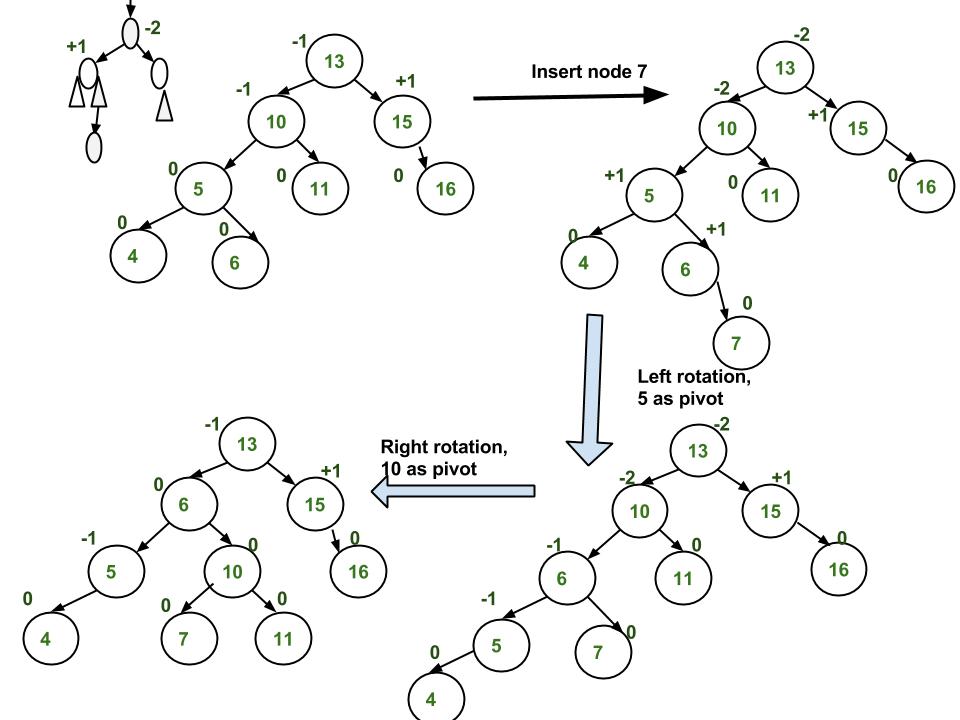
Pada gambar diatas, terdapat sebuah tree yang ditambahkan node yang berisi nilai 7. Node 7 menjadi anak kanan dari 6, karena 7 lebih besar dari 6. Namun bila terjadi hal tersebut, maka balance factor di root akan menjadi +2 atau -2 dan di anak kiri root balance factor akan menjadi +2 atau -2, dikarenakan ruas kiri dari root memiliki kedalaman 4, sedangkan ruas kanan dari root memiliki kedalaman 2 dan juga ruas kanan dari anak kiri root memiliki kedalaman 1, sedangkan ruas kiri dari anak kiri root memiliki kedalaman 4. Karena tidak seimbang, maka dilakukan self-balancing dengan cara mencari bagian yang rusak. Bagian yang pertama yang rusak adalah anak kiridari root, dan yang mengganggu adalah leaf yang memiliki nilai 7. Oleh karena itu angka 5, 6 ,7, kira rotate ke arah kiri atau yang biasa disebut sebagai left rotation untuk memperbaiki rantai. Setelah itu untuk memperbaiki 10 yang memiliki balance factor 2 atau -2, maka dilakukan rotasi kearah kanan atau yang biasa disebut sebagai right rotation. Ambil 3 node diatas dari 10, yaitu 10, 6 , dan 5 setelah itu melakukan right rotation. Setelah itu, 6 menjadi anak kiri dari root, dan tree sudah balance. Inidapat disebut sebagai double rotation.
Delete
Delete memiliki prinsip yang sama dengan Binary Search Tree. Bila ingin menghapus leaf, maka langsung hapus saja. Bila yang ingin dihapus memiliki child, maka child tersebut yang akan menggantikan node yang dihapus. Setelah melakukan delete, maka langkah berikutnya adalah melakukan self-balancing. Prosesnya sama seperti Insert, yaitu melakukan right rotation ataupun left rotation, dan juga bisa melakukan single rotation, maupun double rotation.
Heap and Tries
Pengertian Heap
Heap adalah binary tree yang sudah lengkap yang telah memenuhi persyaratan heap. Berbeda dari AVL Tree, B-Tree, dan Red-Black Tree, Heap tidak memiliki balance factor ataupun warna dalam melakukan rebalancing.
Bentuk Heap
Heap sendiri memiliki dua bentuk umum:
- Min Heap
- Max Heap
Min Heap
Min Heap adalah heap dengan nilai parent lebih kecil dibandingkan nilai childnya. Di dalam tree Min Heap, nilai terkecil terdapat di root, sedangkan nilai terbesarnya terdapat di bagian leaves. Implementasi Min Heap dapat dilakukan di linked list, namun lebih mudah dilakukan dengan menggunakan array. Berikut adalah contoh Min Heap:
Dapat dilihat bahwa nilai parent lebih kecil dibandingkan nilai child nya. Nilai terkecil terdapat pada root, nilai terbesar terdapat di leaves, yaitu 83.
Cara Insert
Cara Delete
Berikut adalah cara delete menggunakan Min Heap yang saya pelajari dari kelas kecil saya. Berbeda dengan Binary Search Tree ataupun AVL, dalam heap nilai yang dihapus SELALU ROOT. Setelah root dihapus maka, ARRAY TERAKHIR akan menggantikan posisi root. Kita tidak menggunakan predecessor ataupun successor. Setelah menjadi root, maka akan melakukan pengecekan dengan childrennya. Ini dapat disebut sebagai down heap atau heapify down. Bila nilai child lebih kecil dari parent, maka akan melakukan balancing dengan cara menukar parent dengan child. Pengecekan ini dilakukan secara rekursif.
Max Heap
Max Heap adalah heap dengan nilai parent lebih besar dibandingkan nilai childnya. berbeda dengan tree Min Heap, dalam tree Max Heap, nilai terkecil terdapat di leaves, sedangkan nilai terbesarnya terdapat di bagian root. Implementasi Max Heap dapat dilakukan di linked list, namun lebih mudah dilakukan dengan menggunakan array. Berikut adalah contoh Min Heap:
Cara Insert
Cara Delete
Pengertian Tries
Tries atau prefix tree adalah tree yang terurut yang dapat menyimpan data array, biasanya berupa strings ataupun char. Kata TRIE berasal dari kata RETRIEVAL karena tries dapat mencari satu kata dalam kamus hanya dengan kata awalan saja. Berikut adalah gambaran tries:
Refrensi:
- https://en.wikipedia.org/wiki/Self-balancing_binary_search_tree
- https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
- https://www.freecodecamp.org/news/avl-tree-insertion-rotation-and-balance-factor/
- https://www.geeksforgeeks.org/avl-tree-set-2-deletion/
- https://www.google.com/url?sa=i&url=http%3A%2F%2Fbtechsmartclass.com%2Fdata_structures%2Ftries.html&psig=AOvVaw39rWJuHg1x0nZIGQLHTz8O&ust=1589618170135000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCMj53aa7tekCFQAAAAAdAAAAABAD
- Binus Maya
No comments:
Post a Comment